The Wonderful World of Enharmonic Spellings

Now that the National Spelling Bee is over for another year I felt compelled to address one of those odd little topics that makes life interesting if you’ve been a crazy musician all of your life and see whether I could take the rest of you along for the ride. If you’ve been wondering what that B-sharp was doing in your perfectly nice piece of piano music when they could have used a C-natural and spared you a little ‘metric conversion’ you’ll soon find out why. Let’s take a trip through the strange world of enharmonic spellings. For indeed, as practiced by composers who know what they are doing, the term 'enharmonics' has everything to do with a kind of musical spelling.

The concept seems simple enough—the term enharmonic equivalent means there is more than one way to refer to the same note. An F natural can also be 'spelled' as an E-sharp. Or a C-flat could be simply a B-natural--or an A double sharp! Under the right conditions, namely if your mind is wired that way, you may enjoy the fact that life sends you another opportunity to escape from the dull routine of having to refer to the same piano key under the same name all the time in perpetuity, but then again, and this probably accounts for the majority of us, you may find it needlessly confusing. The English language is bad enough with its silent gh and its p sounds like f when it comes before h and I before e except after c and on and on until it takes some truly exceptional talents like the kids at the spelling bee to keep track of all the rules and show us all how to do it right. What ever happened to an E is an E is an E, period? Can’t music be the simple language?

It can, and it depends who is using it. In the mists of the past, there were only seven notes to worry about, A through G. An F was an F; there was no such thing as an E-sharp. In those days, if you wanted to 'sharp' something it was a fairly big deal, and wasn’t done willy-nilly with every note in the system (actually, for a while, you could only alter the note ‘B’). Gradually, though, things got more complicated. Although Medieval Music Theory wasn't all that simple to begin with, the necessity of finding a logical way to 'spell' notes came when different systems began to use the same notes for different purposes. At first, a G# wasn't really that same thing as an A-flat--it was actually a different pitch. Then people began tuning things differently, and pretty soon they were in fact the same pitch (more or less--more if you have a piano, and less if you have a non keyboard instrument!) However, that didn't make them the same in other ways, any more than the words 'to', 'two' and 'too' are the same. They sound the same but function differently. Enharmonic pitches can be thought of as musical homophones (they sound the same but look different and mean something different as well). Basically, making the distinction between two notes that can have several different spellings requires knowledge about the musical context, taking into account (1) the overall system in use (the key), (2) the harmonic grouping within that system, and/or (3) the function of a particular note with regard to where it came from and where it is leading. I'm doing my best not to make this sound terribly complicated, though it obviously takes more than five minutes to understand, and, since I have a rash passion for thoroughness, I'm going to take you for a little digression into 'scale creation' to explain the first of those three points: how understanding the key contributes to whether or not to call something an f-sharp or a g-flat. This will be followed by a couple of musical examples to explain the last two points.

Musicians are aware that those seven original notes are not the same distance apart. While most of them are a ‘whole step’ away from each other, there are two places where the notes are only half as far apart, between b and c and again between e and f. On a piano that is easy to see because there are no black keys in between the white notes in these places. Violinists just have to imagine it, poor blokes!

(By the way, if you’re wondered what makes notes a certain distance apart, that has to do with the number of times per second that the sound produces a wave. The higher notes vibrate faster than the lower ones. While they’ve all got numbers (the pitch A above middle c vibrate 440,000 or so times a second, for example) we musicians can’t handle all that math so we simply measure the distance between the notes and leave their actual numerical identity to the piano tuner!)

The fact that those notes are not all at an equal distance apart has given musicians some interesting ways to go about making music. For quite a long time in the ancient world, there were a number of different systems called modes. Basically the way these things worked is that each mode had its own pattern of half-steps and whole-steps in different places in its scale. Tunes that used each mode would sound quite different from one another because the relationship between the notes, largely based on the unequal distances between them, would be different for each mode. It is likely that each town or region had its own mode, and vigorously opposed the others, until eventually, through trade and war, musicians became aware of other modes and increased their melodic vocabulary by trying these wild innovations. By the later centuries folks like Plato complained that we didn’t need all those modes, and really ought to confine ourselves to only two.

He got his wish, eventually. Though the modes persisted through the middle ages (and have actually made quite a comeback in our own two centuries), musicians after about 1600 settled on just two patterns for about 300 years: major and minor. You’ve heard of them!

Now if music had simply eliminated those other modes things would have been easy. Using the white keys alone, one can already play in major and minor, using exactly one pitch as the starting point for the system of notes that makes up each key each time: C major and A minor. The trouble comes in when you want to begin your system on a different note. Suppose C major isn’t exactly your key. You can’t reach the high note without making people leave the room. Or the low note sounds like dry dessert air coming out of your larynx. You’d like to move things up a note or two.

We can do that. The problem is that we now have to add in those ‘extra’ notes—the piano’s black keys (which, incidentally were white when they were first introduced; the white notes were black)—those additional ‘sharps’ and ‘flats’ will help us to preserve the same pattern of half-steps and whole-steps that we had in the key of C, now starting on any note we like (including the black keys). Each major key, for instance, works like this: There are eight notes, and the distance between each note is a whole step, with the exception of the distance between the 3^rd and 4^th note and the 7^th and final note. In C major this is easy. If you use all the white keys from C to C the distance between the 3^rd and 4^th note (E to F) and the 7^th and final note (B to C) is the distance to the very next key on the piano, with no intervening key of either color in between, the very definition of a half-step (if you are using a piano!) But for the key of D you have to make some adjustments to get this same pattern. Instead of preceeding from C to C, we are moving from D to D, using every note in between. In order to get the same pattern of notes in relation to each other (in other words, to make the thing sound like a major scale) two of the notes have to be ‘sharped’:

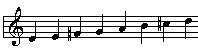
Altering those two notes (the ones with the #s in front of them) means we can sing the standard do-re-mi-fa-sol-la-ti-do the same way we could beginning on C and it will sound just as nice. Doing the same thing for the other notes would require more sharps, or flats, as needed. Now we have a situation were, in trying to simplify things by reducing them to only one pattern, we’re actually made them rather complicated, which is pretty much how life is!

It is at this point where, although knowledge of the pattern should enable one to create any scale for him or herself, without recourse to an answer key, for purposes of this article we will skip over the ‘phonics’ method of ‘sounding out’ each scale, and give you the ‘whole word’ approach, namely, showing you how each major scale is spelled. Note that there is exactly one of each letter of the musical alphabet in each scale (besides the top note, which is a repetition of the bottom). It may be modified by being sharped or flatted, but it will only exist in one incarnation in any scale:

While that might seem like a lot of information (and curiously resemble gene mapping) it is based on a few simple principles, which is terrific if you enjoy simplifying mounds of data with a few sweeping rules to illustrate how it all works. Unfortunately, musician’s minds don’t usually work that way, but here goes anyway:

Each key is a system of notes. No system can have both sharps and flats in it (if you are wondering why, I'll have to save that for another time), so custom and logic have chosen one or the other. For instance, a Gb scale consists only of flatted notes (and one natural one). This is to make things consistent and predictable. I could spell the word "spell" five other ways too, you know, (speghl, spehll, spael, cpewl, ssppel) and by one or another rules of pronunciation, justify the relation between its written representation and the way it is supposed to sound, but custom has agreed on only one. (If you are wondering, the 'gh' is silent in the first one, as in 'light', the 'c' sounds like 's' in the fourth one, as in ceiling, etc.) The idea here is to make things simple and uniform, but the English language has had so many imports from other languages and difference of opinion from various influential persons over how to present it on paper, not to mention a long history and evolution of usage that things have gotten—well, a bit confused. Relatively speaking, music is much better regulated. Relatively, I said.

There are a couple of cases where the starting note of the scale itself can be interpreted enharmonically (i.e., C#/Db, and B/Cb, which is why I gave two scales on the same line. They are the same notes, spelled differently) There aren’t as many cases of this as you would think (only 3, actually). This is because, in order for a scale to work, it must employ one note of each letter name (and only one), and, can only have a sharp, a flat, or a natural version of that letter-named note. Suppose you wanted the re-spell the key of E-flat as D#. In order to preserve the pattern of whole and half steps, the scale would be spelled d#-e#-f-double sharp---whooops! Now as a note f-double sharp is certainly allowed. But in a key signature, something that sets the rules for which pitches are altered at the beginning of the piece, some kind soul determined a while back that double sharps and double flats just weren't welcome. So we can’t have one of those in there. This key will have to go. It is just too darned complicated. Sorry.  This is probably a victory for simplicity, or at least, it keeps complexity from getting totally out of hand. Double flats don’t work in key-signatures, either (or aren't allowed), though they are perfectly acceptable out in the wild (i.e., as accidentals). There are good reasons for having these little miscreants, but they are sufficiently troublesome that their use has been kept to a dull roar (though 19^th century French composers seem to love them to death).

And so we are left with the scales listed above. 15 possible major scales, with their standard spellings. If you are a musician of any seriousness, it is not really that hard to memorize them. You will be stuck with them your entire life.

While the concept of taking a note like C and calling it a D-double flat just because you feel like it seems simple enough (although I don’t know anybody who would do that since it unnecessarily complicates things) when you are writing an actual piece of music you have larger things to consider. This is what students haven’t grasped when they look at a C-flat in a piece of music and wonder why the heck it isn’t just a B-natural.

If you are in the key of G-flat, for instance, the note C-flat belongs to the key, but the note B does not. Intentionally writing a B in place of a C-flat tells a musician who knows something about theory that we are probably not being governed by the rules of the key of G-flat major at the moment. Maybe we’ve left Kansas altogether, or we’re just on a temporary vacation, but one way or another it’s news. If the composer intends to ‘go someplace else’ this is perfectly justifiable, but it not, they’ve just given out false information! Even a musician who doesn’t know anything about theory will probably find things more confusing if the composer ‘spells’ the notes wrong, since, in a lot of cases, things will look more complicated on the page.

Except that sometimes they don’t. In cases where an f-double sharp is required as the leading tone to a G-sharp minor chord, or some other difficult bit of musical spelling, students who aren’t familiar with how the system works tend to get a little upset because they are not thinking within the system in use by the composer (the key) but only of the limited vocabulary they know (which does not include things like f-double sharp!). Why do things get so complicated?

As I’ve tried to indicate, if you understand the way spelling rules operate in music you will actually find correctly spelled notes a blessing, even in cases where you have to read things like f-flat and g-double sharp, because the logic of the system actually makes it easier to understand that way, but since ‘musical grammar’ is so little known even among practicing musicians, concepts like these get lost on most of us.

But if you’ve made it this far into the article, I want to leave you with a couple of musical examples.

The first is from a Mr. Frederic Chopin, whose harmonic progressions are often quite arresting, and original, and not obvious. But Fred knew what he had in mind, and he knew how to spell what he put on paper to make that clear. The little Mazurka (a type of Polish dance) from which I’m about to quote includes several B-double flats in them in the strain before the one you’re going to see. They lead, quite appropriately to A-flats in each case, in the key of Db, which has need of them. Generally speaking, a double flat will always lead down to the next note, and a double sharp will lead up. Since neither is part of the key itself (and not included in the scale) the context is rather important to those little devils. They don’t want to be wrong.

But the place I have in mind is a little transition away from the key of Db back to the key in which he started the piece, f minor. Now Chopin gets us there smoothly by changing only one note, then another, and slowly coaxing us into a new harmonic world with minimal shake-up. In the first of the four measures below is a D-flat chord. All of its notes are accounted for in the key signature, so we don’t need any accidentals.

Next he is going to change it to a D-flat minor chord. This usually causes our spirits to depress a little, but with Chopin you have to enjoy a little melancholy. A D-flat minor chord happens to have an f-flat in it, not an E natural, for just as scales have a standard spelling, so do the chords that come from the scales. Even though the key of f minor (scale: f, g, ab, bb, c, d, e, f, melodically speaking) has an E in it, and not an F - flat, the chord Chopin is using (Db minor), and the key he has not quite left yet , requires him to make it a F - flat. As it happens, reading those notes in the context of the key he is in, I find it much easier with an F - flat in it, because my mind can quickly realize that I am looking at a D-flat minor harmony, and instead of four apparently disconnected individual notes, they all belong to one group. If he'd put an E in there, I would have to figure out how that fit in with the rest of the notes and it would take a little more brain function just to get over the discomfort.

However, in the next bar, Chopin shows us that is he going back to f minor by changing that one note from an F - flat to an E natural. You won’t hear anything change regarding that note. It is the same lever on the piano. But now we are to think of it differently. You see, the bass note has also changed. It is now a C instead of a D-flat. This means we are now on a C-chord, and that is spelled with an E in it, not an F - flat, thank heaven. E also happens to be the 7^th tone of the f minor scale, commonly known as the leading tone, since it is there to lead us up to the F, which is what we are getting ready for in the measure that follows this example. The harmony in the third measure is a little confusing anyway, because Chopin leaves the A-flat in for one more measure. It is there to keep up the tension, and is known as a suspension. Since the A-flat relates to what came before, and the E relates to what is coming up, there is a mixture of different spellings in this measure, but nothing we can't handle! Incidentally, that 'suspension' belongs to a family of items known as 'non-harmonic' tones (not belonging to the current chord) and one of its cousins, the 'appoggiatura' (or leaning tone) was the winning word at the National Spelling Bee a few years ago. (no kidding!)

At last we are ready for F - minor, and if your page turner doesn’t get the page turned fast enough you can guess at it anyway, for the way Chopin has spelled his notes gives us enough of a clue as to what is happening musically that a literate musician knows and can predict what is likely to happen next.

If you’re feeling somewhat dizzy now, take heart. For every person whose mind loves the harmonia that comes from a system of organization that accounts meticulously for every detail, and which prescribes the correct choice of expression for each member of the group, there are some who are not that interested, and they usually include in their number some persons who are famous, and even known for their intellect. The prospect of having a smart, respected person tell us that we should all give our brains a break is a real treat for those of us whose brains bruise easily.

My exemplar of such a stance was an outsider, not trained at a conservatory, and with little patience for those who were. Erik Satie liked to flaunt rules and customs, but it didn’t always result in a greater simplicity, even for people who think a C is always easier to read than a B#, no matter what the context. Satie’s idea of musical spelling included a little sarcasm which caused him to take a simplicity like a C chord and make a monstrously complex thing out of it:

A C-Major chord the way it is normally spelled:	A C-Major chord the way Erik Satie might spell it:

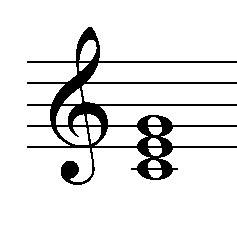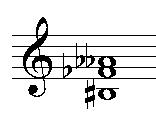It takes a little computation to realize that the chord on the left and the chord on the right sound the same. As for the second one, not only does it not make sense in any likely musical context (and Satie would have made sure it didn’t) but it makes reading a simple chord progression exceedingly difficult. So difficult that one of his most famous pieces defies memorization by the most learned musicians. The oft-repeated observation of those who have played the composer’s Vexations, a short work that is repeated 840 times for upwards of 24 hours, is that even after playing the work through hundreds of times, nobody can memorize the piece. Nor can the musician ever get comfortable with it, since the strangely spelled harmonies require constant concentration to ‘translate’ them into more comprehensible patterns. Sometimes the same chord is spelled three different ways to facilitate this abstraction.

Satie wasn’t doing this through ignorance, though the results might have been somewhat similar if he had been (with the exception of his imaginatively spelled C chord, surely!). Probably he was poking fun at what he thought was a stuffy and arcane bunch of rules, and, considering the double-sharp- and double-flat-happy culture that surrounded him, it is not hard to feel sympathy for his position.

The results, however are of a different order entirely. They even manage to do for this professional musician, schooled in the most difficult classical repertoire, what the very idea of enharmonic spellings does for musicians who have not become acquainted with the concept or learned to understand it, when confronted with an example like Chopin’s, or innumerable others which feature B#s or A-double flats on the basis of correct theory or spelling—it gives me a headache!